静密封条件下Y形橡胶密封圈有限元分析-emc体育油封
来源: 发布时间:2020-01-17 16:58
静密封条件下Y形橡胶密封圈有限元分析
ginite Element Analysis on Rubber Sealing Y-ring in the Condition of Static Sea
摘要:针对在静密封条件下使用的一种新型义形橡胶密封圈,利用大型有元软件 ANSYS对形密封图在不同工作压力下的变形与受力情况进行了有限元分析,得出了相应的 Von-Mises 应力分布及接触压力分布,并预测了Y形密封圈可能出现裂纹的位置,总结了Y形密封圈接触压力的变化规律。
y形橡胶密封圈主要用干液压系统中活塞、注塞和活塞杆的密封。为获得初始密封,在设计Y形密封圈时,内、外唇有一定的过盈。当密封圈装入沟槽中,达到密封的效果。在压力作用下,由于密封唇圆周方向的变形,产生接触压力,随着液体压力的增加,变形和接触压力也随之增加,Y形圈达到自封效果··· ·· 。作者在研制一种非刚性连接输油管道新型连接器时,设计了一种Y形橡胶密封圈(非标准件)作为连接器的密封件,所要求的密封状态为静密封。为了验证其使用性能,传统的方法是研制出实物橡胶圈进行试验,研究其密封性能是否满足要求,这种方法费时费力,效率低下。为了提高设计效率,节约研究成本,本文作者提出采用大型有限元分析软件AN-SYS对所设计的Y形密封圈进行有限元分析,通过分析密封圈的应力、接触压力和形变来考察其密封性能。
1.Y形密封圈有限元分析模型
1. 1橡胶材料的应力应变关系
橡胶从本质上说是一种粘弹性材料,其力学特性与时间及温度有关,即呈现出蠕变、松弛、老化等现象。然而,当时间较短且温度变化不大时,则可认为橡胶材料是完全弹性的,即当载荷被撤走后,橡胶材料完全恢复到它未变形的状态。在密封结构中,其力学模型表现为复杂的材料非线性和几何非线性。
AN-SYS非线性超弹性模型主要有PolynomidForm模型、Mooney.Rivlin模型、Neo-Hookean模型、Yeoh模型、Arruda-Boyce模型、Gent模型、Ogden模型、Hyperfoam 模型、Blatz.Ko模型旧1.目前在ANSYS中广泛
采用Mooney-Rivlin模型描述橡胶材料的应变能函数。
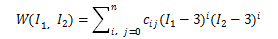 (1)式中:w为修正的应变能,c。为Rivlin系数,,l、2分别为第1、第2Green应变不变量。
(1)式中:w为修正的应变能,c。为Rivlin系数,,l、2分别为第1、第2Green应变不变量。
本文作者利用ANSYS进行有限元分析时,采用两常数的Mooney.Rivlin模型,则式(1) 变成:
 (2)式中:c 。 。和c0。为Rivlin系数,均为正定常数。
(2)式中:c 。 。和c0。为Rivlin系数,均为正定常数。
1. 2接触问题的有限元分析
接触问题Ho的复杂性是由于系统状态的改变,即由物体间的接触、分离造成的,故接触问题又被称为状态非线性问题。目前,各国学者提出了许多接触问题的有限元算法,如Lagrange乘子法、罚单元法以及基于求解器的直接约束法等。本文作者采用罚单元法,罚单元法就是在两接触面的各节点间建立一种伪
单元来模拟面与面的接触。从变分角度看,罚单元法是将结构的总势能II表达为应变势能形、外力势能E和接触力势能Q的和呤1.即:
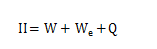
(3)通过罚单元给出Q的表达式,从而解决接触面被穿透的问题。

1. 3 有限元模型的建立
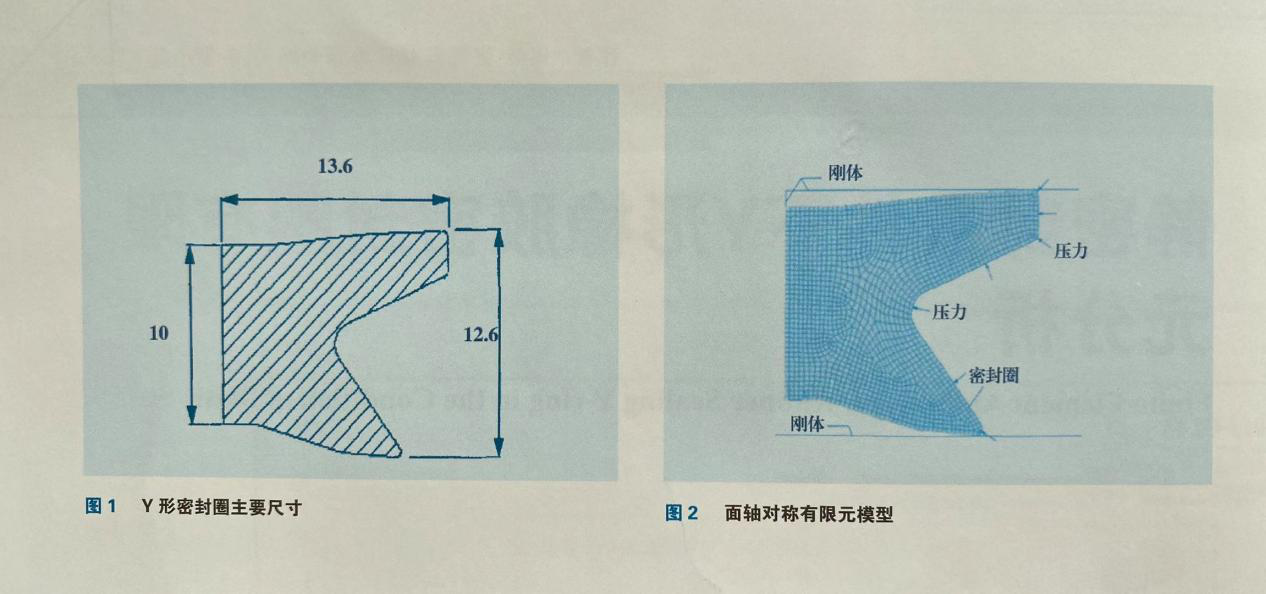
基本假设: (1) 由于钢构件构成的密封槽壁的刚度是橡胶的几万倍,所以不考虑其变形,将其视为刚体边界。 (2) 认为Y形圈的橡胶材料不可压缩。 (3) 橡胶密封圈及接触边界均按轴对称问题处理,取Y形圈和密封槽壁的二维截面进行研究。Y形橡胶密封圈材料为丁橡胶(NBR) , 硬度为IRHD (国际橡胶硬度等级)85, 其主要设计尺寸如图1所示。工作压力为0~3MPa.
橡胶单元采用实体单元PLANEI183, 分析中采用的橡胶材料模型为近似不可压缩弹性材料的Mooney-Rivlin模型函数,其应变能偏量部分有关的2个材料常数c, 。和c。。分别为1.87和0.47”1。模型中的接触对由接触单元CONTAI72和目标单元TARGEI69配对组成,沟槽边界用刚体来模拟。模型网格划分如图2所示。

2 计算结果与分析
利用大型有限元软件ANSYS对Y形密封圈在不同工作压力下的变形与受力情况进行了有限元分析,得出了相应的范·米塞斯(Von-Mises) 应力分布及接触压力分布。
2. 1 Y形密封圈装配时的分析
当刚体达到装配位置(工作压力P=0) , Y形密封圈被挤压,压缩量为1.1mm.其压缩形变、Von- Mises应力、接触压力分布如图3、4所示。从图中可以看出,最大Von-Mises应力出现在上下唇交汇处,达到了1。33MPa, 上下唇部的最大接触压力均
有0.57MPa。
2. 2不同工作压力时Y形密封圈的Von-Mises 应力
Von-Mises应力反应了Y形圈截面上各主应力差值的大小。一般来讲,应力值越大的区域,材料越容易出现裂纹。此外,应力越大,将加速橡胶材料的松弛,从而造成“刚度”下降。Von-Mises
应力子为:
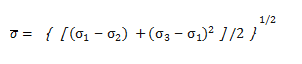 (4)
(4)
式中:a1、a2、a3, 为单元体3个方向的主应力。
考虑到密封圈的工作压力为0-3MPa, 本文中选取了0。5, 1, 1。5, 2, 2。5, 3, 3。5, 4, 4。5, 5MPa10 个不同压力进行分析,具体统计数据见表1.从表1可以看出,随着工作压力的增加,最大Von-Mises 应力值逐步增加。图5, 6为低压(1MPa) 和高压(5MPa) 作用下Y形圈的Von-Mises应力图。与低压时相比,高压作用下Y形圈剖面上的Von-Mises
应力也明显增加,上下唇交汇处达到了5。8MPa.同时可以发现Von-Mises应力峰区的位置发生了变化,并且主要集中在Y形圈下部倒角处。这说明在不同工作压力下Y形圈下部倒角处最可能出裂纹。

2. 3不同工作压力时Y形密封圈的接触压力
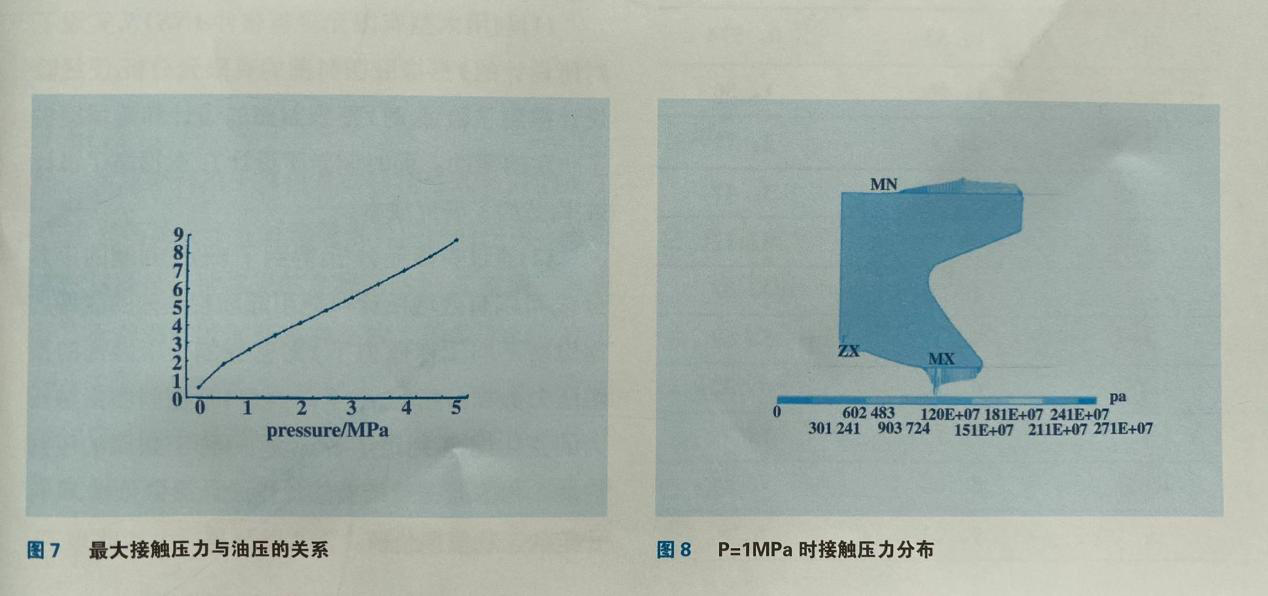
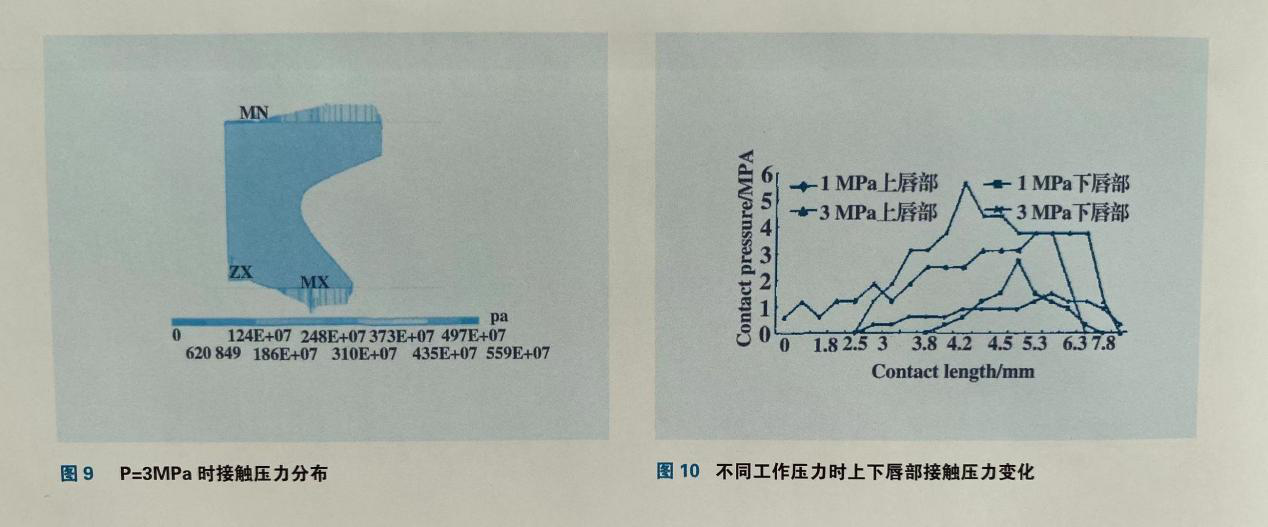
Y形圈的密封面为上下唇部,本文中主要分析了上下唇部的接触压力。接触压力的大小反应了Y形圈的密封能力,Y形圈保证密封的必要条件是密封界面上的最大接触压力大于或等于油压。0。5~5MPa10个等级工作压力下的最大接触压力如
表1所示。且从图7可以看出,随着油压的增加,最大接触压力亦随之增加,呈线性关系,其值总是大于油压。从图8, 9可以看出,接触压力的峰值总是出现在下唇部,并且上唇部的接触长度总是大于下唇部接触长度。图10为P=1, 3MPa时上下唇部接触压力变化图,接触压力分布呈类似二次曲线变化,下唇部接触压力突变比较明显。
3.结论
(1) 利用大型有限元分析软件ANSYS, 实现之对所设计的Y形橡胶密封圈的有限元分析,使经验设计得到了验证,对Y形密封圈的设计和选型提供了一定的帮助。同时创新了设计方法,提高了设计效率,节约了研究成本。
(2) 通过有限元分析,得到了Y形密封圈的应力分布,可以有效地估计可能引起断裂失效的区域。通过对不同工作压力下Y形密封圈上下唇部的接触压力数据分析,总结了该类型Y形密封圈接触压力的变化规律,判定了各工况下Y形密封圈的密封性能。为橡胶密封结构的优化设计提供依据,具有一定的工程应用价值。
如果您需要更换关于采购信息欢迎您与emc体育油封联系。

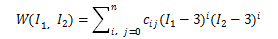

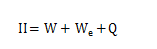



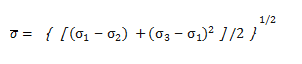 (4)
(4)
